Eksponen atau bilangan berpangkat adalah konsep penting dalam matematika yang sering digunakan dalam berbagai bidang seperti ilmu pengetahuan alam, teknik, dan ekonomi. Memahami eksponen sangat penting karena membantu dalam menyederhanakan perhitungan dan memecahkan masalah yang kompleks dengan lebih mudah.
Jika teman-teman ingin belajar tentang eksponen, kebetulan kali ini admin akan membahas tentang apa itu eksponen, serta sifat-sifat penting yang harus dipahami.
Apa itu Eksponen (Bilangan Berpangkat)?
Eksponen adalah konsep matematika yang digunakan untuk menunjukkan berapa kali suatu bilangan, yang disebut basis, dikalikan dengan dirinya sendiri. Ketika kita menggunakan eksponen, kita mengatakan bahwa basis tersebut akan “dipangkatkan” dengan eksponen tertentu.
Misalnya, jika kita memiliki bilangan 2 pangkat 3, ini berarti kita mengalikan angka 2 sebanyak 3 kali, yaitu 2 × 2 × 2.
Konsep eksponen bermanfaat dalam matematika karena memungkinkan kita untuk mengungkapkan perkalian berulang dengan cara yang lebih ringkas. Sebagai contoh, daripada menulis 2 × 2 × 2 × 2 untuk bilangan 2 pangkat 4, kita dapat menulisnya sebagai 2^4.
Ini membuat perhitungan menjadi lebih efisien dan mudah dipahami.
Selain itu, eksponen juga digunakan dalam berbagai bidang ilmu pengetahuan dan teknologi. Misalnya, dalam fisika, eksponen digunakan untuk menghitung pertumbuhan eksponensial dalam populasi atau penurunan radioaktif dalam bahan kimia.
Dalam ekonomi, eksponen digunakan untuk menghitung laju pertumbuhan investasi atau penurunan nilai tukar mata uang.
Dengan pemahaman yang baik tentang eksponen, kita dapat menyederhanakan perhitungan matematika yang kompleks dan memahami lebih dalam konsep-konsep yang melibatkan perkalian berulang dalam berbagai konteks kehidupan sehari-hari dan ilmiah.
Sifat-Sifat Eksponen
Pangkat Penjumlahan
Sifat pertama dari eksponen adalah pangkat penjumlahan. Dalam kasus ini, jika kita memiliki dua bilangan dengan basis yang sama dan eksponen yang berbeda, kita dapat menjumlahkan eksponen tersebut.
Rumusnya adalah:
am . an = am + n
Ini berarti bahwa ketika kita mengalikan dua bilangan yang memiliki basis sama, kita cukup menambahkan eksponennya.
Pangkat Pengurangan
Sifat berikutnya adalah pangkat pengurangan. Dalam hal ini, jika kita membagi dua bilangan dengan basis yang sama, kita dapat mengurangkan eksponen dari bilangan tersebut.
Rumusnya adalah:
am : an = am – n
Pangkat Perkalian
Sifat ini berlaku ketika sebuah bilangan berpangkat dipangkatkan lagi. Dalam hal ini, kita harus mengalikan eksponennya.
Rumusnya adalah:
(am)n = am x n
Perkalian Bilangan yang Dipangkatkan
Jika dua bilangan yang berbeda dipangkatkan kemudian dikalikan, maka masing-masing bilangan tersebut dipangkatkan secara terpisah.
Rumusnya adalah:
(a . b)m = am . bm
Perpangkatan pada Bilangan Pecahan
Untuk bilangan pecahan yang dipangkatkan, pembilang dan penyebut masing-masing dipangkatkan. Rumusnya adalah:
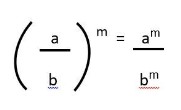
Pangkat Negatif
Pada sifat ini, jika eksponen positif diubah menjadi negatif atau sebaliknya, bilangan tersebut dipindahkan posisinya dari pembilang ke penyebut atau sebaliknya. Rumusnya adalah:
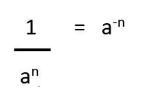
Pangkat Pecahan
Pangkat pecahan adalah sifat eksponen di mana eksponennya adalah pecahan. Dalam hal ini, penyebut pecahan menjadi akar dan pembilang menjadi eksponen dari hasil akar tersebut. Rumusnya adalah:
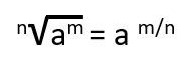
Pangkat Nol
Sifat eksponen yang terakhir adalah pangkat nol, di mana setiap bilangan yang dipangkatkan nol hasilnya adalah satu, dengan syarat bilangan tersebut bukan nol. Rumusnya adalah:
a0 = 1
Penutup
Memahami konsep eksponen dan sifat-sifatnya adalah dasar penting dalam matematika yang dapat diaplikasikan dalam berbagai bidang. Dengan pemahaman yang baik tentang eksponen, kita dapat menyederhanakan perhitungan yang kompleks dan memahami lebih dalam tentang matematika dan ilmu pengetahuan lainnya.
Teruslah berlatih dan eksplorasi lebih banyak soal-soal eksponen untuk meningkatkan pemahaman teman-teman.

