Tentu kamu pernah belajar tentang bangun ruang di sekolah kan? Atau malah sekarang sedang di materi pembelajaran ini? Yap, pelajaran matematika yang satu ini termasuk materi yang gak pernah absen dari kurikulum.
Tapi, walau dari kecil kita sering menemui bentuk-bentuk dari bangun ruang, nyatanya masih banyak yang bingung pas harus ngejelasin apa itu bangun ruang secara gamblang. Apalagi pas kita mau ngitung, apa coba rumusnya?
Jadi, kalo kamu sedang mempelajari tentang bangun ruang, baik dari jenis maupun rumusnya, kebetulan kali ini admin sedang membahas materi ini.
Karena gini, belajar matematika itu sebenarnya gak sesusah yang dibayangin, asal kita tahu pendekatan yang pas dan logika di baliknya. Termasuk pas mempelajari bangun ruang, yang sebenarnya sering kita temui di kehidupan sehari-hari.
Apa Itu Bangun Ruang?
Kita mulai dari pertanyaan paling dasar dulu ya, apa coba bangun ruang itu?
Sederhananya, bangun ruang adalah bentuk geometri tiga dimensi yang memiliki isi atau volume. Berbeda dengan bangun datar yang hanya terdiri dari panjang dan lebar, bangun ruang memiliki kedalaman alias tinggi, jadi bisa dihitung volumenya.
Bayangkan kalo bangun datar itu kayak ngegambar bentuk persegi di kertas, maka bangun ruang adalah versi real-nya di dunia nyata—misalnya kardus berbentuk kubus atau balok. Jadi, bangun ruang itu bisa dipegang dan diisi, tak hanya dilihat aja.
Setiap bangun ruang memiliki bagian-bagian, di antaranya..
- Sisi, yaitu permukaan datar yang membentuk bangun ruang itu
- Rusuk, adalah garis pertemuan antara dua sisi
- Titik sudut, yaitu titik tempat tiga rusuk bertemu
Contoh paling gampang dadu, dadu adalah contoh nyata dari bangun ruang kubus. Dari dadu kamu bisa ngelihat 6 sisi berbentuk persegi, 12 rusuk yang menghubungkan sisinya, dan 8 titik sudut di tiap pojoknya.
Sifat-Sifat Bangun Ruang
Sebenarnya tiap bangun ruang punya ciri khasnya masing-masing. Tapi secara umum, semua bangun ruang memiliki beberapa sifat dasar yang pasti dimiliki, diantaranya..
- Punya volume
Bangun ruang itu bisa diisi, misal kamu bisa ngisi botol air (yang bentuknya menyerupai tabung) dengan cairan. Inilah yang dimaksud dengan volume. - Ada rusuk
Rusuk itu semacam tulang punggung dari bangun ruang. Tanpa rusuk, sisi-sisi dari bangun ruang gak bisa nyatu. - Memiliki titik sudut
Titik sudut ini adalah tempat di mana tiga atau lebih rusuk bertemu. Kamu bisa lihat titik sudut ini di pojok-pojok bangun seperti kubus atau balok. - Punya bidang sisi
Adalah permukaan yang membentuk bangun ruang itu sendiri. Bisa datar, kayak pada kubus dan balok, atau melengkung seperti pada bola dan tabung.
Jenis-jenis Bangun Ruang
1. Kubus
Kubus adalah bentuk sempurna dari bangun ruang yang simetris dan teratur. Semua sisinya itu persegi dan ukurannya sama persis, makanya disebut juga bentuk yang kongruen.
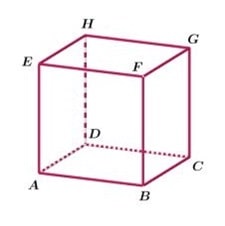
Sifat-sifatnya dari kubus diantaranya..
- Memiliki 6 bidang sisi yang semua bentuknya persegi dan berukuran sama. Jadi sisi depan, belakang, atas, bawah, kiri, dan kanan bener-bener sama.
- Memiliki 12 rusuk yang semuanya sama panjang, inilah garis-garis yang menghubungkan sisi satu dengan sisi lainnya.
- Titik sudutnya ada 8, seperti pada ujung-ujung dari kotak kado—nah itu dia titik sudutnya.
- 12 diagonal sisi—jadi di setiap sisi persegi bisa kamu narik dua garis diagonal dari sudut ke sudut berseberangan.
- 4 diagonal ruang, inilah garis yang menghubungkan dua titik sudut yang saling berseberangan dalam satu ruang.
2. Balok
Kalau balok masih mirip-mirip kubus, tapi dengan bentuk yang lebih fleksibel. Karena tak semua sisinya harus persegi, tapi tetap simetris.
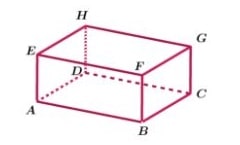
Berikut sifat-sifat dari balok..
- Punya 12 rusuk, dibagi jadi 3 kelompok rusuk sejajar yang masing-masing memiliki 4 rusuk. Rusuk yang satu panjang, yang satu lagi pendek, sesuai dimensi balok.
- 6 bidang sisi, terdiri dari 3 pasang sisi kongruen. Artinya, sisi depan sama dengan sisi belakang, sisi atas sama dengan bawah, dan sisi kiri sama dengan kanan—tapi bentuknya bisa persegi panjang.
- 8 titik sudut sama kayak kubus, ujung-ujung balok ini tempat pertemuan tiga rusuk.
- 12 diagonal sisi, karena setiap sisi berbentuk persegi panjang, kamu bisa narik 2 diagonal di masing-masing sisi.
- 4 diagonal ruang, yaitu garis yang menghubungkan dua titik sudut yang berseberangan secara diagonal dalam ruang balok.
Kalau kamu lihat kardus minuman atau kotak sepatu, itulah contoh balok. Jadi, bentuknya memang familiar dan banyak di sekitar kita.
3. Tabung
Bangun ruang yang satu ini bentuknya unik karena sisi-sisinya melengkung. Gak kayak kubus atau balok yang semua sisinya datar, tabung justru memiliki sisi lengkung sebagai pembungkusnya.
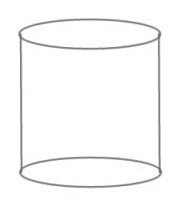
Sifat-sifat dari tabung sendiri sbb..
- 2 rusuk berbentuk lingkaran—rusuk di sini maksudnya bukan garis tepi tajam ya, tapi lebih ke tepi atas dan bawah yang membentuk lingkaran.
- 3 bidang sisi: ada dua lingkaran di alas dan atas, plus satu sisi tegak yang bentuknya melengkung alias selimut tabung.
- Diameter dan jari-jari lingkaran alas dan atas sama besar, karena tabung itu bentuknya simetris vertikal.
- Tinggi tabung adalah jarak antara pusat lingkaran alas ke pusat lingkaran di atas.
Kamu bisa liat benda-benda berbentuk tabung seperti kaleng minuman atau botol termos.
4. Kerucut
Kerucut bentuknya mirip kayak topi ulang tahun atau cone es krim, bentuknya tajam di satu titik, dengan alasnya yang bundar.

Sifat-sifat kerucut diantaranya..
- 2 bidang sisi: satu berupa lingkaran (sebagai alas), dan satu lagi selimut kerucut yang melengkung dari pinggir alas ke puncak.
- 1 rusuk yang berupa lingkaran alas.
- Tinggi kerucut adalah jarak dari puncak ke pusat lingkaran alas—biasanya ditarik lurus ke bawah.
- Ada yang namanya garis pelukis (sering dilambangkan sebagai TA), yaitu jarak dari puncak ke titik mana pun di tepi lingkaran. Untuk menghitung luas permukaan kerucut.
5. Limas
Selanjutnya ada limas, yang dibatasi oleh segi-n (bentuk datar seperti segitiga, segiempat, dll) di alasnya, dan bagian atasnya menyatu di satu titik puncak.
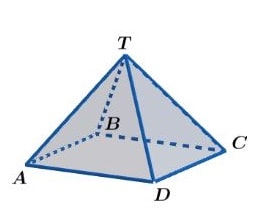
Macam-macam limas tergantung dari bentuk alasnya, bisa limas segitiga, limas segiempat, limas segilima, ada juga limas segienam. Dan sifat-sifatnya diantaranya sbb..
- Jumlah rusuknya ada 2n, artinya kalau alasnya segiempat (n = 4), maka rusuknya ada 8.
- Jumlah sisi tergantung dari bentuk alas, karena tiap sisi tegak berbentuk segitiga.
- (n + 1) bidang sisi, satu alas + n sisi tegak, misal limas segiempat punya 5 sisi.
- (n + 1) titik sudut, karena puncaknya jadi tambahan dari titik sudut di alas.
Contoh dari limas di dunia nyata adalah bentuk dari piramida di Mesir, yang merupakan bentuk dari limas segiempat.
6. Bola
Nah kalo ini laki-laki mesti pada tau, bangun ruang yang paling bulat dan tanpa sudut, bola. Bola tak memiliki sisi datar sama sekali, jadi beda dari bangun-bangun ruang lainnya.
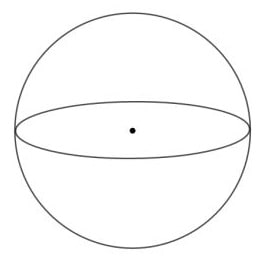
Sifat-sifat bola diantaranya..
- Memiliki 1 bidang sisi dan itu melengkung sempurna.
- Gak punya rusuk maupun titik sudut, jadi kamu tak akan menemui garis atau pojokan di bola.
- Punya jari-jari (r), yaitu jarak dari titik pusat bola ke permukaan.
Cara Mengamati Bangun Ruang
Setelah tau berbagai bangun ruang dan sifatnya, sekarang admin jelaskan bagaimana cara mengamati dan mengenali bentuk bangun ruang. Terkadang, bentuk-bentuk ini gak bisa langsung kamu lihat dalam wujud nyata, tapi bisa kamu bayangkan atau bentuk sendiri dari benda sehari-hari.
1. Pergerakan Objek
Cara pertama, kamu tinggal amati bagaimana sebuah bangun datar bisa bergerak dan berubah jadi bangun ruang.

Bayangin kamu punya selembar kertas segitiga yang kamu letakkan di atas meja. Terus, kamu angkat segitiga itu secara tegak lurus dari meja setinggi 10 cm, lalu buat permukaan baru sejajar dengan alasnya.
Tanpa sadar, kamu telah membuat bentuk prisma segitiga.
Dengan cara ini, kamu bisa menghidupkan bangun datar dan membayangkannya menjadi bentuk ruang. Cara ini bermanfaat bagi yang tipe belajarnya visual dan kinestetik, karena bisa ngebayangin bentuk dari gerakan.
2. Jaring-Jaring Bangun Bervolume
Pasti kamu pernah membuat jaring-jaring waktu sekolah kan? Kertas berbentuk pola yang setelah dilipat-lipat jadi kubus atau limas, itulah yang namanya jaring-jaring bangun ruang.
Dari sini kamu bisa mengenali setiap sisi, rusuk, dan sudut dari bangun ruang, bahkan sebelum bentuknya jadi. Kamu pun juga lebih gampang memahami struktur bangun itu sendiri.
Misalnya, jaring-jaring kubus pasti punya 6 persegi yang semuanya ukurannya sama. Tapi kalau kamu membuat jaring-jaring balok, kamu bakalan nemu 3 pasang persegi panjang yang berukuran sama tapi beda panjangnya.
3. Proyeksi
Sedangkan cara ini lebih teknis dan biasa digunakan dalam gambar teknik atau arsitektur.
Proyeksi adalah teknik melihat bentuk bangun ruang dari sudut tertentu—biasanya dari tampak atas, tampak depan, atau tampak samping. Mirip kayak kamu lagi ngegambar bentuk 3D di kertas 2D.
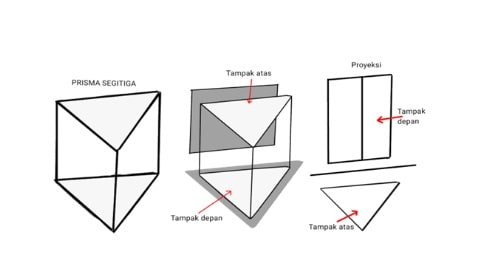
Contohnya gini, kamu punya model balok yang kamu amati dari atas, yang terlihat cuma bentuk persegi panjang. Tapi kalau kamu lihat dari samping, bisa jadi tampilannya beda lagi tergantung ukuran tingginya.
Dengan teknik proyeksi ini, kamu bisa menganalisis dan membayangkan struktur bagian dalam suatu bangun tanpa harus membongkar fisiknya.
Rumus Volume Bangun Ruang
Sekarang untuk rumus-rumus perhitungan volume dari berbagai bentuk bangun ruang, silahkan temen-temen simak dibawah ini..
| Bangun Ruang | Rumus Volume |
Kubus | V = r x r x r Keterangan |
Balok | V = p x l x t Keterangan |
Prisma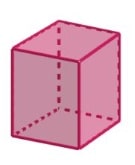 | V = Luas alas x tinggi |
Limas | V = 1/3 x Luas alas x tinggi |
Tabung | V = π x r x r x t Keterangan |
Kerucut | V = 1/3 x π x r x r x t Keterangan |
Bola | V = 4/3 x π x r x r x r Keterangan |
Penutup
Oke temen-temen, mungkin sampai disini admin bisa memberi penjelasan tentang materi bangun ruang. Semoga apa yang admin sampaikan dapat membantu kalian lebih memahami dan gak bingung lagi saat ketemu soal-soal bangun ruang di sekolah.
Inget, memahami bangun ruang tak hanya pada rumusnya aja, tapi juga bagaimana cara kita melihat bentuk-bentuk di sekitar kita dengan lebih jeli.

