Dalam dunia matematika, terdapat konsep yang sangat penting dan mendasar yang dikenal sebagai relasi, fungsi, domain, kodomain, dan range. Konsep-konsep ini memiliki peran sentral dalam berbagai bidang matematika serta memiliki aplikasi yang luas dalam dunia nyata.
Dalam artikel ini, kita akan menggali dengan lebih dalam mengenai konsep-konsep tersebut dan bagaimana mereka berinteraksi satu sama lain.
Pengertian Relasi
Relasi adalah konsep dasar yang menghubungkan dua set elemen yang mungkin memiliki hubungan tertentu di antara mereka. Dalam konteks ini, elemen-elemen ini bisa berupa angka, objek, atau bahkan konsep abstrak lainnya.
Relasi diwakili oleh pasangan nilai dari kedua set tersebut. Misalnya, jika kita memiliki set A berisi {1, 2, 3} dan set B berisi {x, y, z}, kita dapat memiliki relasi {(1, x), (2, y), (3, z)}.
Pengertian Fungsi
Fungsi adalah jenis khusus dari relasi yang memiliki sifat tertentu. Fungsi menghubungkan setiap elemen dari satu set (domain) ke elemen tunggal di set lain (kodomain). Ini berarti setiap input memiliki tepat satu output.
Fungsi sering kali direpresentasikan dalam bentuk persamaan matematika. Sebagai contoh, f(x) = 2x merupakan fungsi yang mengaitkan setiap bilangan dalam domain dengan dua kali nilai tersebut.
Pengertian Domain, Kodomain, dan Range

a. Domain
Dalam matematika, domain merujuk pada himpunan semua nilai input yang valid untuk suatu fungsi atau relasi. Dalam konteks fungsi, domain merupakan kumpulan nilai yang dapat dimasukkan sebagai input ke dalam fungsi untuk menghasilkan output yang berhubungan. Dengan kata lain, domain adalah rentang nilai yang dapat “dimakan” oleh fungsi tersebut.
Misalnya, jika kita memiliki fungsi f(x) yang menghitung akar kuadrat dari x, maka domainnya akan berisi semua nilai real non-negatif, karena tidak mungkin menghitung akar kuadrat dari bilangan negatif dalam hal ini.
b. Kodomain
Kodomain, dalam matematika, adalah himpunan semua nilai yang mungkin menjadi output dari fungsi atau relasi tertentu. Ini mencakup semua kemungkinan nilai yang bisa diberikan oleh fungsi, terlepas dari apakah nilai-nilai ini benar-benar tercapai atau tidak.
Sebagai contoh, jika kita memiliki fungsi g(x) yang menghitung kuadrat dari x, maka kodomainnya adalah semua bilangan real, karena potensialnya adalah menghasilkan bilangan real apapun sebagai output.
c. Range
Range, juga dikenal sebagai jangkauan atau gambar fungsi, adalah subset dari kodomain yang terdiri dari nilai-nilai yang benar-benar dihasilkan oleh fungsi untuk beberapa nilai input di dalam domain. Ini adalah kumpulan nilai yang sebenarnya dapat dicapai oleh fungsi.
Misalnya, jika kita memiliki fungsi h(x) yang menghitung kuadrat dari x dengan domain semua bilangan real dan kodomain semua bilangan real positif, maka range h(x) akan berisi semua bilangan real positif.
Contoh:
[(1,3), (2,4), (3,5), (3,7), (4,5)] tentukan domain, kodomain dan range dari relasi tersebut
Jawab :
Domain: 1,2,3,4,
Kodomain: 3,4,5,7,
Range: 3,4,5,7
Contoh Soal Relasi dan Fungsi
1. Relasi
Setiap anggota dari suatu himpunan asal dapat memiliki pasangan dengan lebih dari satu anggota dari himpunan lainnya, atau bahkan tidak mempunyai pasangan sama sekali. Relasi antara dua himpunan dapat dinyatakan melalui tiga cara berikut:
- Diagram panah
- Diagram Cartesius
- Himpunan pasangan berurut
Mari kita amati perbedaan antara tiga cara tersebut melalui contoh berikut!
Contoh Kasus Relasi
Misalkan kita mempunyai himpunan A = {1,2,3,4,5} dan himpunan B = {2,3,4,5,6,7,8,9,10}!
a. Diagram Panah
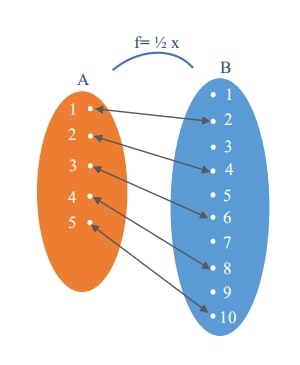
Cara paling sederhana dalam menyatakan suatu relasi adalah melalui diagram panah. Dalam metode ini, relasi digambarkan dalam bentuk panah yang menghubungkan anggota himpunan A ke anggota himpunan B.
b. Diagram Cartesius

Diagram Cartesius terdiri dari sumbu X dan sumbu Y. Anggota himpunan A diwakili oleh sumbu X, sedangkan anggota himpunan B diwakili oleh sumbu Y. Relasi antara himpunan A dan B ditunjukkan oleh titik-titik atau noktah di dalam diagram.
c. Himpunan Pasangan Berurut
Relasi antara dua himpunan bisa dinyatakan dalam bentuk himpunan pasangan berurut. Dalam metode ini, anggota himpunan A ditulis di depan, sedangkan anggota himpunan B yang dipasangkan ditulis di belakang.
Contoh Kasus Relasi di atas bisa diringkas sebagai berikut:
A = {1,2,3,4,5} dan B = {2,3,4,5,6,7,8,9,10}!
Sehingga Himpunan Pasangan Berurutnya adalah:
{(1,2), (2,4), (3,6), (4,8), (5,10)}
2. Fungsi
Fungsi sering direpresentasikan dengan huruf kecil seperti f, g, h, i, dan lainnya. Fungsi f memetakan anggota himpunan A ke anggota himpunan B, dan dapat dituliskan sebagai f(x): A→B.
Sebagai contoh, kita bisa memiliki fungsi f yang memetakan A ke B dengan aturan f: x → 2x + 2.
Membaca Notasi Fungsi
Dalam notasi f(x) = 2x, x adalah anggota domain. Arti dari notasi x → 2x adalah bahwa setiap anggota x dari domain dipetakan menjadi 2x. Dengan demikian, daerah hasil x oleh fungsi f adalah 2x. Dalam notasi f(x) = 2x, kita menyatakan bahwa fungsi f memetakan x ke 2x.
Contoh Soal Fungsi
Misalnya kita memiliki fungsi f: x → ax + b, dengan x adalah anggota domain f. Dalam hal ini, rumus fungsi f adalah: F (x) = ax + b
Misalnya: Diketahui f(x) = x² + 3 dengan {x|–3 ≤ x ≤ 3}. Tentukan domain fungsi f dan range fungsi f.
Jawab:
Domain Fungsi f = {-3, -2, -1, 0, 1, 2, 3}
Range (Daerah hasil) f(x) =
f (-3) = x² + 3 = (-3)2 + 3 = 12
f (-2) = x² + 3 = (-2)2 + 3 = 7
f (-1) = x² + 3 = (-1)2 + 3 = 4
f (0) = x² + 3 = (0)2 + 3 = 3
f (1) = x² + 3 = (1)2 + 3 = 4
f (2) = x² + 3 = (2)2 + 3 = 7
f (3) = x² + 3 = (3)2 + 3 = 12
Hasil f(x) dapat pula dinyatakan dalam diagram panah, koordinat Cartesius, atau himpunan pasangan berurut.
Pentingnya Konsep-Konsep Ini
Konsep-konsep relasi, fungsi, domain, kodomain, dan range memiliki peran penting dalam berbagai aspek matematika dan aplikasinya dalam dunia nyata.
- Matematika Diskret: Dalam matematika diskret, konsep relasi digunakan untuk memodelkan hubungan di antara objek-objek terpisah. Misalnya, dalam teori graf, relasi menghubungkan simpul-simpul dalam graf.
- Kalkulus dan Analisis: Dalam kalkulus, fungsi digunakan untuk menganalisis perubahan dan laju perubahan. Domain, kodomain, dan range membantu kita memahami batasan dan dampak dari fungsi.
- Ilmu Komputer: Konsep-konsep ini menjadi dasar penting dalam ilmu komputer, terutama dalam pemrograman dan pengembangan algoritma. Fungsi dan relasi sering digunakan dalam struktur data dan pemrosesan informasi.
Penutup
Dalam dunia matematika, konsep relasi, fungsi, domain, kodomain, dan range memiliki peran yang signifikan dalam menganalisis dan memahami hubungan antara elemen-elemen. Dalam artikel ini, kita telah membahas pentingnya konsep-konsep ini dalam berbagai bidang matematika dan aplikasinya dalam kehidupan sehari-hari.
Dengan pemahaman yang kuat tentang konsep-konsep ini, kita dapat mengambil langkah lebih maju dalam memahami matematika dan menerapkan pengetahuan ini dalam berbagai konteks.
Dengan tuntas, artikel di atas menjelaskan konsep-konsep kunci dalam matematika, yaitu relasi, fungsi, domain, kodomain, dan range. Artikel ini menjelaskan konsep dengan rinci dan memberikan contoh nyata untuk mengilustrasikan setiap konsep.
Dengan memahami konsep-konsep ini, pembaca akan memiliki dasar yang kuat dalam menerapkan matematika dalam berbagai konteks.

