Tabung adalah salah satu bentuk geometri yang sering kita temui dalam kehidupan sehari-hari. Dari gelas hingga pipa, bentuk tabung sangat berguna dan sering digunakan.
Untuk memahami lebih dalam mengenai tabung, kita perlu mengetahui beberapa sifat dan rumus yang terkait dengan volume, luas permukaan, dan keliling alas tabung.
Apa itu Tabung?

Tabung adalah salah satu bentuk bangun ruang yang paling dikenal dan sering digunakan dalam berbagai aplikasi sehari-hari. Dalam matematika, tabung dikenal dengan nama silinder.
Bentuk dasar tabung terdiri dari dua alas berbentuk lingkaran yang identik dan sebuah selimut berbentuk persegi panjang yang melingkari lingkaran tersebut. Tabung memiliki simetri yang unik dan beberapa sifat yang membedakannya dari bentuk geometri lainnya.
Secara umum, tabung dapat digambarkan sebagai objek tiga dimensi yang memiliki tinggi (h) dan jari-jari (r) pada alas lingkarannya. Tabung bisa ditemukan dalam berbagai bentuk dan ukuran dalam kehidupan sehari-hari, seperti gelas, pipa, kaleng, dan lain-lain.
Penggunaan tabung sangat luas karena bentuknya yang sederhana namun efisien untuk menyimpan atau mengalirkan cairan serta benda-benda lainnya.
Sifat-Sifat Tabung
Tabung memiliki beberapa sifat unik yang penting untuk diketahui. Berikut adalah beberapa sifat utama dari tabung:
- Memiliki alas dan tutup yang berukuran sama:
Kedua alas tabung berbentuk lingkaran dan memiliki jari-jari yang sama. Ini berarti kedua lingkaran tersebut memiliki luas dan keliling yang sama. - Memiliki 2 rusuk:
Rusuk pada tabung adalah garis lurus yang menghubungkan kedua alas. Rusuk ini biasanya disebut sebagai tinggi tabung (h). - Memiliki 2 bidang:
Tabung terdiri dari dua bidang utama, yaitu dua lingkaran (alas dan tutup) dan satu persegi panjang (selimut). Bidang lingkaran adalah alas dan tutup tabung, sedangkan bidang persegi panjang adalah selimut yang melingkari tabung. - Tidak memiliki titik sudut:
Berbeda dengan bangun ruang lainnya seperti kubus atau balok yang memiliki sudut-sudut tajam, tabung tidak memiliki titik sudut. Hal ini disebabkan oleh bentuk alas dan tutupnya yang melingkar.
Sifat-sifat ini membuat tabung menjadi bentuk yang sangat efisien untuk berbagai keperluan, terutama dalam menyimpan dan mengalirkan benda-benda yang berbentuk cair atau gas.
Bagian-Bagian Tabung
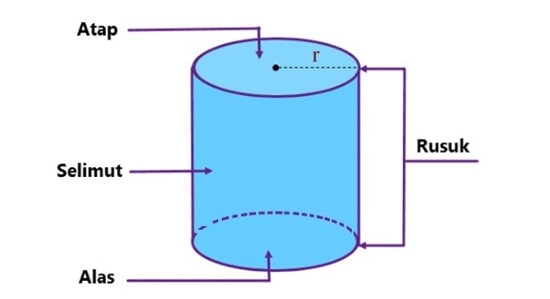
Untuk memahami lebih dalam tentang tabung, kita perlu mengetahui bagian-bagian yang menyusunnya. Berikut adalah penjelasan mengenai bagian-bagian utama dari tabung:
1. Alas dan Tutup
Alas dan tutup tabung adalah dua lingkaran yang identik dan sejajar satu sama lain. Kedua lingkaran ini memiliki jari-jari yang sama dan terletak pada ujung-ujung tabung.
Lingkaran ini menjadi dasar dan penutup dari tabung, sehingga disebut sebagai alas dan tutup.
Contoh: Jika sebuah tabung memiliki jari-jari 5 cm, maka alas dan tutupnya adalah lingkaran dengan jari-jari 5 cm.
2. Selimut Tabung
Selimut tabung adalah bidang persegi panjang yang melingkari kedua lingkaran (alas dan tutup). Panjang dari selimut ini adalah keliling lingkaran (2πr), dan lebarnya adalah tinggi tabung (h).
Ketika selimut ini direntangkan, ia akan membentuk persegi panjang dengan panjang 2πr dan lebar h.
Contoh: Jika sebuah tabung memiliki jari-jari 5 cm dan tinggi 10 cm, maka selimut tabungnya adalah persegi panjang dengan panjang 2π(5) cm dan lebar 10 cm.
3. Tinggi Tabung
Tinggi tabung adalah jarak antara alas dan tutup tabung. Tinggi ini merupakan salah satu ukuran penting yang menentukan volume dan luas permukaan tabung.
Tinggi tabung diukur sepanjang rusuk yang menghubungkan kedua lingkaran.
Contoh: Jika sebuah tabung memiliki tinggi 10 cm, maka jarak antara alas dan tutupnya adalah 10 cm.
a. Rumus Luas Permukaan Tabung
Luas permukaan tabung adalah jumlah luas dari dua lingkaran (alas dan tutup) ditambah dengan luas selimut tabung. Rumus untuk menghitung luas permukaan tabung adalah:
V = π.r².t
Keterangan:
- V Luas Permukaan Tabung
- π (pi) adalah konstanta yang mendekati 3,14 atau 22/7
- r adalah jari-jari alas tabung
- t adalah tinggi tabung
- . adalah kali (X)
Cara Menghitung Luas Permukaan Tabung
Untuk menghitung luas permukaan tabung, kita perlu menghitung dua bagian utama:
- Luas dua lingkaran (alas dan tutup)
- Luas selimut tabung
Langkah-langkah Menghitung Luas Permukaan Tabung:
- Hitung luas dua lingkaran:
Luas satu lingkaran adalah πr². Karena ada dua lingkaran, maka luas kedua lingkaran adalah 2πr². - Hitung luas selimut tabung:
Selimut tabung adalah persegi panjang dengan panjang keliling alas (2πr) dan lebar tinggi tabung (h). Jadi, luas selimut adalah 2πrh. - Jumlahkan kedua luas tersebut:
Luas permukaan tabung = 2πr² + 2πrh.
Contoh Soal:
Sebuah botol minum berbentuk tabung memiliki diameter 14 cm dan tinggi 25 cm.
Diketahui: diameter alas tabung (d) = 14 cm, berarti jari-jarinya adalah 1/2 kali diameternya, yaitu 7 cm. Kemudian, tinggi tabung (t) = 25 cm.
Maka, cara menghitung luas permukaannya sebagai berikut..
Lp = 2πr (r + t)
Lp = 2 (22/7) (7) (7 + 25)
Lp = 44 (32)
Lp = 1408 cm2
Jadi, luas permukaan tabung atau botol minum adalah 1408 cm2.
b. Rumus Volume Tabung
Volume tabung adalah ruang yang dapat ditempati oleh tabung tersebut. Rumus untuk menghitung volume tabung adalah:
V = 2πr (r + t)
Keterangan:
- V adalah volume tabung dalam kubik
- π (pi) adalah konstanta yang mendekati 3,14
- r adalah radius atau jari-jari alas tabung
- t adalah tinggi tabung
- . adalah kali (X)
Cara Menghitung Volume Tabung
Untuk menghitung volume tabung, kita perlu menghitung luas alas tabung terlebih dahulu, kemudian mengalikannya dengan tinggi tabung.
Langkah-langkah Menghitung Volume Tabung:
- Hitung luas alas:
Luas alas tabung adalah πr² - Kalikan luas alas dengan tinggi tabung:
Volume tabung = π.r².t
Contoh Soal:
Sebuah tabung memiliki jari-jari sepanjang 7 cm dengan tinggi 35 cm akan diisi air. Berapa volume air yang dapat ditampung tabung tersebut?
Diketahui jari-jari tabung (r) = 7 cm dan tinggi tabung (t) = 35 cm. Maka penyelesaiannya sebagai berikut..
V = π.r2.t
V = (22/7).(72).(35)
V = 5390 cm3
Jadi, volume air yang dapat mengisi tabung tersebut adalah sebesar 5390 cm3.
c. Rumus Keliling Alas/Tutup Tabung
Keliling alas atau tutup tabung adalah panjang dari garis tepi lingkaran yang membentuk alas atau tutup tabung. Rumus untuk menghitung keliling alas/tutup tabung adalah:
Keliling Alas/Tutup Tabung = 2πr
Keterangan:
- π (pi) adalah konstanta yang mendekati 3,14.
- r adalah jari-jari alas tabung.
Cara Menghitung Keliling Alas/Tutup Tabung
Untuk menghitung keliling alas atau tutup tabung, kita hanya perlu mengalikan diameter lingkaran (2r) dengan π.
Langkah-langkah Menghitung Keliling Alas/Tutup Tabung:
- Kalikan diameter dengan π: Keliling alas/tutup = 2πr.
Contoh Soal:
Jika sebuah tabung memiliki jari-jari 7 cm, maka keliling alas/tutupnya adalah:
Keliling = 2π(7)
K = 2 π r
K = 2 × 22/7 × 7
K = 308/7
K = 44 cm
Penutup
Dengan memahami rumus-rumus dan cara menghitung luas permukaan, volume, serta keliling alas tabung, kita dapat lebih mudah dalam menyelesaikan berbagai masalah yang berkaitan dengan tabung dalam kehidupan sehari-hari maupun dalam bidang studi.
Semoga apa yang admin sampaikan kali ini memberikan manfaat ya untuk teman-teman yang mungkin sedang mencari rumus tabung dan yang ingin meningkatkan pemahaman mengenai tabung.

