Apakah kamu berangan-angan, bagaimana cara mudah menentukan nilai rata-rata dari sebuah set data? Atau bagaimana menemukan nilai tengah yang bisa mewakili data tersebut? Dan bagaimana mengetahui nilai yang paling sering muncul?
Dalam dunia statistika, konsep mean, median dan modus sangat penting untuk memahami distribusi data. Dengan ketiga konsep tersebut, kamu bisa dengan mudah menjawab semua pertanyaan diatas.
Karena itu jika kamu ingin belajar, kali ini admin akan membegikan informasi tentang pengertian mean, median, dan modus serta memberikan contoh cara menghitungnya dengan langkah-langkah yang mudah dipahami.
Jadi, tak usah berlama-lama lagi ya. Yuk langsung saja ke pembahasan mean, median dan modus!
Apa itu Mean (Rata-Rata)?
Mean, atau rata-rata, adalah salah satu ukuran pemusatan data yang paling umum digunakan. Mean dihitung dengan menjumlahkan semua nilai dalam satu set data dan kemudian membaginya dengan jumlah nilai tersebut.
Konsep mean sangat berguna dalam berbagai bidang, seperti pendidikan, bisnis, dan penelitian, karena memberikan gambaran umum tentang data yang dianalisis.
Cara Mencari Mean
- Jumlahkan semua nilai dalam satu set data.
- Hitung jumlah total nilai tersebut.
- Bagilah jumlah total nilai dengan jumlah nilai yang ada.
a. Rumus Mean Data Tunggal (Tidak Berkelompok)
Rumus mean untuk data tunggal secara matematis sebagai berikut..
Mean = (x1 + x2 + x3 + … + xn) / n
Keterangan :
- x1, x2, x3, … xn = jumlah semua nilai data
- n = banyaknya data
b. Rumus Mean Data Kelompok (Distribusi Frekuensi)
Rumus mean data kelompok berbeda dengan rumus mean data tunggal. Berikut rumus mean data kelompok..
Mean = (x1.f1 + x2.f2 + … + xn.fn) / (f1 + f2 + … fn)
Keterangan :
- x1, x2, x3, … = nilai tengah
- f1, f2, f3, … = frekuensi
Bisa juga ditulis dalam bentuk sigma untuk mempersingkat, biasanya soal yang terdapat data diinput dalam bentuk tabel.
Untuk rumusnya sebagai berikut..
Mean = ∑ xi.fi / fi
Keterangan :
- xi = nilai tengah kelompok ke-i
- fi = frekuensi kelompok ke-i
Contoh Soal Mencari Mean
Berikut adalah data nilai ulangan Sejarah kelas 7, cari berapa banyak siswa yang nilainya diatas rata-rata.

Penyelesaian:
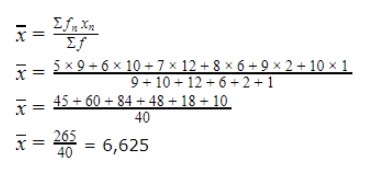
Dari hasil diatas, didapati nilai rata-ratanya adalah 6,625. Karena yang ditanya banyak siswa yang nilainya di atas rata-rata, maka kita dapat hasilnya 7 sampai 10, dengan total siswa sebanyak 21 siswa.
Apa itu Median (Data Tengah)?
Median adalah nilai tengah dalam satu set data yang telah diurutkan. Jika jumlah data ganjil, median adalah nilai yang berada di tengah. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
Median sangat berguna untuk menggambarkan distribusi data yang mungkin memiliki nilai ekstrem atau outlier, karena median tidak dipengaruhi oleh nilai-nilai ekstrem tersebut.
Cara Mencari Median
- Urutkan data dari nilai terkecil hingga terbesar.
- Jika jumlah data ganjil, ambil nilai yang berada di tengah.
- Jika jumlah data genap, ambil dua nilai tengah dan hitung rata-ratanya.
1. Rumus Median Data Tunggal (Tidak Berkelompok)
Pertama, urutkan data dari yang terkecil ke terbesar. Lalu tentukan banyaknya data (lambangkan dengan “nt”). Untuk mencari median, pehatikan apakah “nt” itu genap atau ganjil.
Jika nt ganjil maka menggunakan rumus..
a. Rumus Median data berjumlah Ganjil
Median = 2n / 2
Keterangan :
- n = nilai tengah
Jika nt genap menggunakan rumus..
b. Rumus Median data berjumlah Genap
Median = (n1 + n2) / 2
Keterangan :
- n1, n2 = nilai tengah yang bersebelahan
2. Rumus Median Data Berkelompok
Median = Tb + {(n/2) – fk} x p / fKeterangan :
- Tb = tepi bawah kelas median
- n = jumlah frekuensi
- fk = frekuensi kumulatif
- f = frekuensi kelas median
- p = panjang kelas interval
Contoh Soal Mencari Median
a. Median Data Ganjil
Median dari data: 7, 8, 8, 9, 4, 3, 7, 9, 5, 7, 6, 5, 6 adalah …
Penyelesaian:
3, 4, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9, 9
n =13 termasuk data ganjil, kamu bisa menggunakan rumus median untuk data ganjil..
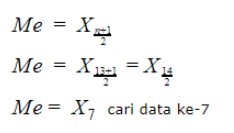
Maka kita mendapat nilai mediannya adalah 7.
b. Median Data Genap
Cari median dari data berikut..

Penyelesaian:
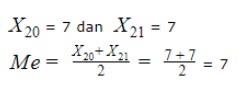
Dari hasil diatas, kita mendapati nilai mediannya adalah 7.
Apa itu Modus (Nilai yang Sering Muncul)?
Modus adalah nilai yang paling sering muncul dalam satu set data. Modus dapat memiliki lebih dari satu nilai jika beberapa nilai muncul dengan frekuensi yang sama.
Modus memberikan informasi tentang nilai yang paling umum atau populer dalam satu set data, yang bisa sangat berguna dalam analisis tren atau pola.
Cara Mencari Modus
- Hitung frekuensi kemunculan setiap nilai dalam satu set data.
- Identifikasi nilai yang memiliki frekuensi kemunculan tertinggi.
1. Rumus Modus Data Tunggal
Rumus modus data tunggal hanya perlu mencari frekuensi data yang paling banyak muncul. Misalkan kita memiliki data sebagai berikut..
102, 106, 107, 108, 107, 105, 108, 107, 102, 105, 106,
106, 105,106, 107, 106, 105, 102, 106, 106, 105, 107.
Hitung frekuensi kemunculan:
- 102: 3 kali
- 105: 5 kali
- 106: 7 kali
- 107: 5 kali
- 108: 2 kali
Nilai yang muncul paling sering adalah 106 (7 kali). Jadi, modus dari data tersebut adalah 106.
2. Rumus Modus Data Berkelompok
Sedangakan untuk rumus modus data kelompok sebagai berikut..
Modus = Tb + {d1 / (d1 + d2)} x pKeterangan :
- Tb = tepi bawah
- d1 = selisih frekuensi modus dengan frekuensi sebelumnya
- d2 = selisih frekuensi modus dengan frekuensi sesudahnya
- p = panjang kelas interval
Contoh modus data berkelompok

Dari data diatas, kita mendapati modus dengan frekuensi paling banyak adalah pada kelas interval 40 – 60 dengan frekuensi 12 kali.
Penyelesaian:
Tb = 40 – 0,5 = 39,5
p = 20
d1 = 12 – 10 = 2
d2 = 12 – 6 = 6
Modus = Tb + {d1 / (d1 + d2)} x p
= 39,5 + {2 / (2 + 6)} x 20
= 39,5 + (1/4) x 20
Modus = 39,5 + 5
= 44,5
Jadi, modusnya adalah 44,5
Penutup
Mean, median, dan modus adalah konsep dasar dalam statistika yang sangat berguna untuk analisis data. Dengan memahami dan mampu menghitung ketiganya, kita bisa mendapatkan wawasan yang lebih dalam tentang distribusi data dan membuat keputusan yang lebih tepat berdasarkan data tersebut.

